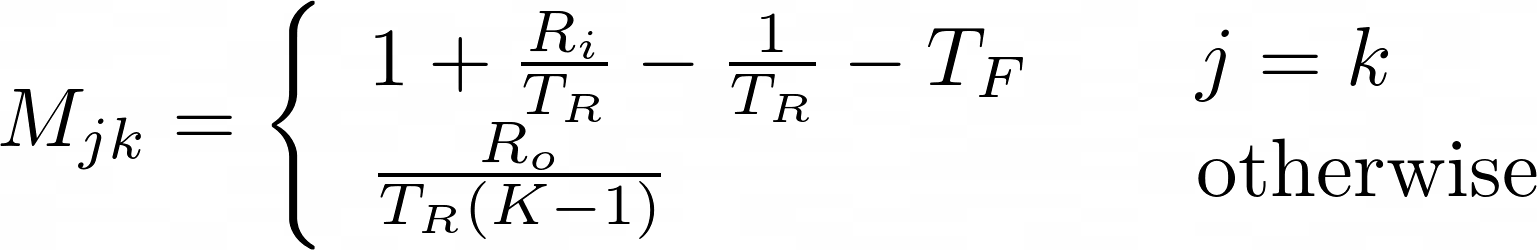Rules of Thumb for Reopening

Part 4: Pod people

We are now approximately two and a half months into the lockdown and we have learned at least one undeniable truth: human beings are not cut out for social distancing. The good news is that many of us are not completely socially isolated. We are fortunate to live with a few members of our immediate families where the rules of social distancing are relaxed; within our households we can interact in a “normal” way. As campuses contemplate opening in the Fall, it is tempting to think about whether there could be analogous social structures in campus life. In this week’s post we will consider: Who is our “family” on a college campus? And what implications does that have in the spread of the virus?

To address these questions, consider small units of people, a.k.a. “pods.” Within each pod, social distancing is diminished much like social distancing is relaxed between immediate family members at home. Unfortunately (and unsurprisingly) there is no free lunch; if we loosen social distancing protocols within the pods, we have to make up for that luxury elsewhere.

As in the opting out post, the criterion for a system of pods to be stable can be derived via an eigenvalue calculation (see details in the “ … mathematically inclined … “ section below). This criterion turns out to be exactly what one might expect from the queuing argument presented in our original post on testing namely:

R_in + R_out ≤ 1 + T_FT_R

where R_in and R_out represent the number of people one contagious person infects inside and outside their pod, respectively. As in the previous posts, T_F is the fraction of the population tested daily and T_R is the number of days an infected person is contagious. Here we have saved ourselves some typing and assumed that everyone is asymptomatic; this estimate is likely to be conservative (but it is easy enough to add symptoms back into the mix following the arguments in our original post). These R’s can be further dissected by noting that they are proportional to the number of contacts per day with the infected person, N_i, and the probability that each contact becomes infected, p_i, e.g. R_i = p_iN_iT_R.

Designing pods

So far, everything we have described is independent of the details of the pod structure. In the following we will use this as a starting point to explore the implications of different pod designs. At the highest level, there are three types of pod architectures that one might consider. First, there are systems with a large number of pods and a large number of people per pod. In that context, the stability criterion from the eigenvalue analysis presented above is appropriate. Next, there is the limit of a large number of pods each containing a finite (small) number of people (e.g. roommates). In that limit, the relevant “stability” of the system is dictated by spread of the virus between pods. Even if the disease spreads extremely rapidly within a pod, the system-level stability can be maintained by decreasing interpod interactions such that the pod boundaries serve as “firewalls” (i.e. it is ok to infect your roommate as long as you and your roommate are sufficiently socially distanced from other people on campus). In this limit, we can take a pod-centric view of the universe in which the pods are considered to be the relevant “unit” in our network and the criterion above reduces to a more lenient condition

R_out ≤ 1 + T_FT_R

The third architecture is a small number of pods each containing a large number of people; in this case it is the stability of the internal dynamics that largely determines the stability of the system. In the following we will focus on the pod-centric view (although the results are easily generalizable to the other two cases).

The pod-centric approach also allows us to focus on the limit where the infection spreads relatively rapidly within each pod; under those conditions, there is a high probability that the state of all of the people in a pod is identical (i.e. if I am infected, then it is extremely likely that my roommates are also infected and vice versa). In this limit, if we test one person in the pod, we have learned the state of approximately everyone in the pod which adds a multiplier to our effective testing fraction (with the caveat that T_F cannot exceed 1 unless we test multiple times per day), hence T_F → min(XT_F,1) where X is the number of people in the pod. This multiplier encapsulates the epidemiological benefit of podding: we pay a price in increasing transmission by relaxing interactions within the pod but, if T_F is high enough, we may recover that cost in information which allows us to easily find additional infected individuals.

Finally, we have to accept that none of these pods will be perfectly isolated; the consequent interpod interactions (a.k.a. “leakiness”) are captured in R_out. There are any number of forms that the interpod interactions could take (e.g. a fixed number of interactions per pod per day, or leakiness that scales with the number of people per pod to some power X^a, etc.… ). In this post we will assume that everyone is equally likely to leak. Consider two pods, one that is infected and contains Infected Ivan, and one that is susceptible. The likelihood that Ivan infects someone in the susceptible pod scales like X, the number of people in the susceptible pod (i.e. roll a dice for Susceptible Susan, Sam, Silas, etc. who each have a very small probability of becoming infected); this is true for all X people in Ivan’s pod so the probability of Ivan’s pod infecting another pod scales like X². Then there are a total of (K-1) susceptible pods just like this one that Ivan’s pod could potentially infect, where K is the total number of pods in the population. For pods that are well-described by these criteria, the stability condition becomes:

p_out X² (K-1) T_R ≤ 1 + min(XT_F,1) T_R

This condition can now be used to address practical questions around constructing pods.

Roommates

One of the most frequent questions we are asked is whether there is a difference in the spread of the virus if students are housed in single rooms versus doubles. In particular, if we allow students to live in doubles, does that change the social distancing requirements between non-roommates?

Since X is small in this case (e.g. 2 for doubles, 3 for triples, etc) we will consider XT_F ≤ 1. Rearranging the stability criterion above to quantify the limits on p_out, i.e. the acceptable level of interaction (or noncompliance) between non-roommates, we find

p_out ≤ ( 1 + XT_R T_F ) / [ X² (K-1) T_R]

This reduces to our original stability criterion when X = 1 and, as expected, rooming with a buddy reduces your allowable external social interaction budget (by a factor of about 1/X if XT_RT_F » 1). Note that this factor is highly dependent on the form one chooses in modeling external interactions. For example, if one chooses R_out to be linear in X instead of quadratic, the denominator in this relationship scales like X instead of X²; then the number of people per pod is largely irrelevant and you can in theory pile as many people into a pod as you like (up to XT_F ≤ 1) without dramatically reducing interpod interactions. (But be forewarned that if you design your pods assuming such a linear relationship, and the increase in R_out with X turns out to be faster than linear, your large seemingly stable pods will turn out to be very problematic.)

Upper limit on pod size

The second question we often receive is: What is the largest pod size we can implement without compromising the stability of the system? In that case, X is likely to be large so we take min(XT_F, 1) = 1. Then the pod-level stability criterion can be arranged to find the maximum allowable number of people per pod:

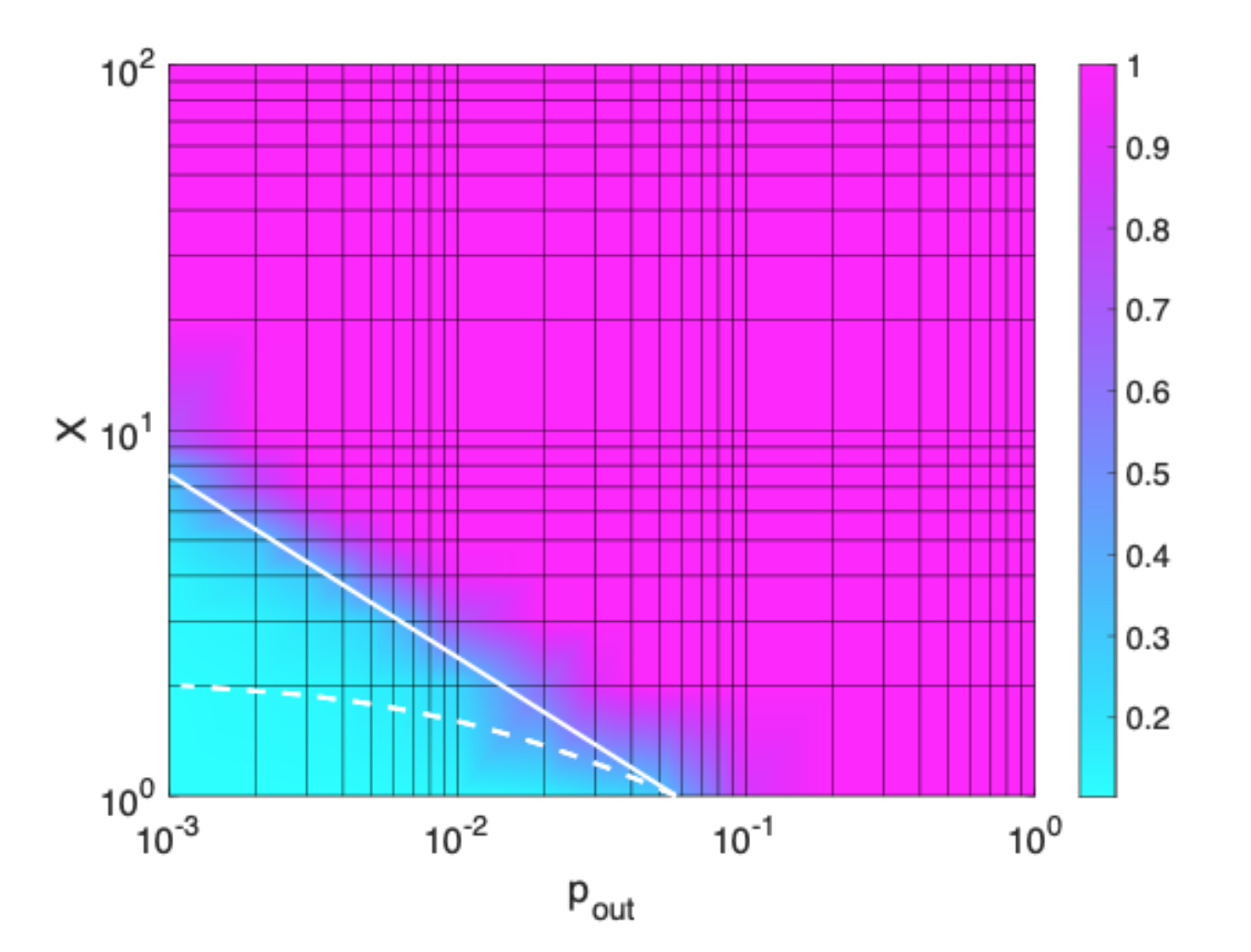
X_max = [ (1 + T_R) / (p_out (K-1) T_R) ]^1/2

This criterion is shown in the plot below (white line) along with MCMC simulation data; color indicates average fraction of the population recovered at steady state in the stochastic simulation; the dashed white line indicates the stability criterion including interpod interactions (i.e. including p_i). Again as expected, as the size of the pod increases, the interpod social distancing must increase to make up for the increased intrapod interactions. Hence larger pods can be stabilized by making p_out small.

Are pods a good idea?

Maybe. The challenge with pods is that if we let the virus spread, the virus will spread. The concept at the heart of the pods is that we are giving license to allow spread in a limited capacity (i.e. within the pod). Any protocol that includes “allowing spread” as part of the design should raise a warning flag during a pandemic. Even if the spread is contained within a pod, the more people there are in an infected pod, the greater the odds of leaking to other pods.

That being said, we can also not forget that pods are comprised of people, which brings us back to the assertion at the beginning of this post: people are not cut out for social distancing. Although pods may increase transmission, the benefits associated with increased happiness in living as a social unit (and the associated increased likelihood of compliance with rules and other guidance) may out-weight the hit we take to R_out. If pods are carefully constructed and paired with appropriate well-designed testing protocols, the increase in spread appears to be manageable and may be worth the trade-off.

Derivation of the stability criterion of the full system for the mathematically inclined

Consider a modified SIQR model, in which each individual belongs to one of K pods. Let I_k,n be the number of members of the k^th pod who are infectious at time n. We will assume the worst case, where all members of the population are susceptible to infection. We can write the system of evolution equations of the infected populations as:

where the state transition matrix M has the form

with parameters as defined and discussed above as well as in our original post on testing.

We consider the disease controlled if the number of infections is stable (constantly decreasing). Stability occurs when the eigenvalues of the transition matrix M are less than 1. The maximum eigenvalue of M is

The stability criterion is then

R_i + R_o ≤ 1 + T_FT_R

as discussed above.

For further details please contact: Munzer Dahleh, Sarah Fay, Peko Hosoi, Dalton Jones.