Rules of Thumb: Adjusting Class Schedules in Fall Term ’20
Inside spaces such as lecture halls and lab spaces bring an elevated risk of transmission of COVID-19. The foundation on which university schedules are built, whom to bring together in inside spaces becomes a challenge. This guide highlights parameters and decisions that university administrators will make: which classes to offer to which students, online or offline.
Why the Problem is Important
Student schedules are increasingly interdisciplinary. With increasing numbers of double majors and breadth-of-study requirements, students have interacted with different other students pre-COVID-19. In normal settings, this allows for enriching intellectual stimulation. In post-COVID-19’s new normal, however, these spaces of interaction need to be re-thought.
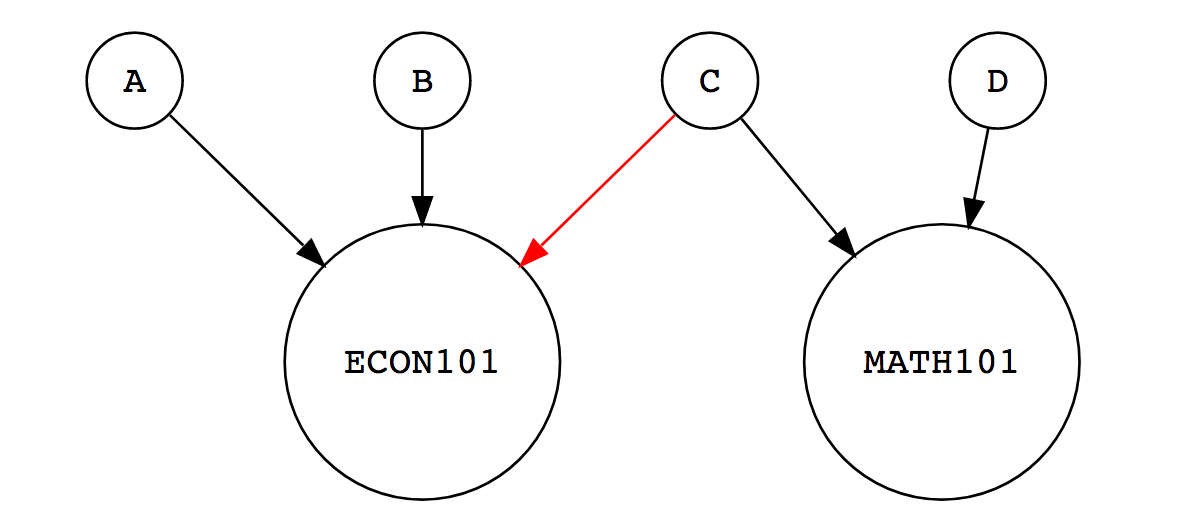
A helpful abstraction can be the network mapping students to classes that they take. As an example, consider Alice (A), Bob (B), Claire (C) and Daniel (D) that take at most two classes (ECON-101, MATH-101). Alice, Bob and Claire take ECON-101, Claire and Daniel take MATH-101. We can depict this using arrows connecting students to classes if they take a class.
It is impossible to find any clustering that at the same time (a) allows all students to take all of their classes on-site (b) to not allow infections of one student to all others through meetings in classes (potentially through an intermediate infection). A “solution” would be to ask Claire to take ECON-101 on-line, or to offer two sections of ECON-101 or MATH-101 (then with a section with only one student).
Partitioning students into groups, called pods, that only take classes—or sections of classes—can limit the spread of the virus, and, at the same time, allow students social interaction within their pod without breaking social distancing guidelines. Additional sections of classes to allow for pods could be done both physically (by having students from different cohorts sit separately) or temporally (by having professors give multiple times the class in sub-sections).
This comes not for free, and some students will need to take classes on-line, and more sections of classes will be necessary if the mixing of students in closed spaces should be minimized. The rest of this article highlights important choices in designing schedules that are compatible with small pods, and gives a case study in which MIT calibrates the feasibility of pods of size 50 for its classes with an essential on-site component. (We emphasize that groups of 50 students will not be epidemiologically stable – non-overlapping groups of this size allow, at least, for easier testing and contact tracing, and will give the administration a margin to partially reduce social distancing measures.)
Policy Parameters
Important decisions that need to be made are
- Which classes are “essential”? In a first step, decisions should be made which classes are crucially on-site. We outline considerations on student and class size for these decisions.
- Which classes should even then be offered in an alternative form? Some classes are such a central meeting point of students that even with only offering essential classes, these would need very many sections to allow for small pods. We present a quantitative heuristic for the selection of these courses.
- How many students should form a pod? We name considerations for deciding on the size of pods.
- How to decide on how many sections of a class to offer? Once the classes to be offered (and, depending on this selection, students to bring back to campus) are chosen, the assignment of students to pods is considered. We show below how this can be done using clustering algorithms.
- Should we ask students for their pod preferences? We show below, and in an appendix why asking students for their preferences leads to non-satisfactory outcomes.
The rest of this section gets into each of the five points more in detail.
Finding Essential Classes
Some classes can be offered online more easily than others. For example, a robotics lab class will need to alter the structure much beyond installing discussion rules in a lecture. Classes where transition is feasible should not be labelled as essentially on-site.
But this is not the only consideration in defining essential classes. Also students’ academic progress should be factored in. Some students might take crucially on-site classes outside of their major and their connection to a course could be determined as “non-essential”. When allowing students efficient means to request one of their classes to be classified as essential for them, this allows to efficiently reduce the number of student-class pairs on-site.
Finding Central Classes
In some cases, there might be some margin on what classes can be considered “essential”. In this case, it can be helpful to identify classes that would expose the most students directly or indirectly with the virus in determining how much effort should be put into transforming classes to on-line instruction.
Network theory (the science of entities and their connections) has operationalized the ranking of connection of different parts of the network. Some important ones:
- eigenvector centrality, that can be defined recursively: A class is central if it is taken by many central students; a student is central if they take many central classes.
- betweenness centrality, that identifies students or classes that connect otherwise loosely/not connected clusters.
Identifying classes and negotiating with faculty offering the classes can allow to reduce the number of sections of a class—and increase the number of students per section—to make the COVID-19 schedule more efficient.
Deciding on Pod Sizes
The pod size should be informed by estimates of the basic reproductive number R0 inside and outside of pods. If pods are so large that an infection inside a pod becomes very likely, then testing and quarantine capacity might be too limited to sustain the pods. On the other hand, too small pods might make very many sections of a class necessary.
Besides these capacity considerations, also social aspects might be relevant in the decision on pod sizes: Students should be able to sustain their social life in a non-socially distanced fashion on campus, too small pods might limit these opportunities for students.
Deciding on Sections
With the remaining essential, non-central classes, the administration needs to assign students to pods. Formally, this is a (balanced) Graph Partition problem, which is computationally hard, even though there are solvers for it. Informed by observation in data below, we give a (sub-optimal) rule of thumb.
(Not) Eliciting Pod Preferences
It might be tempting to ask students for their preferences on who they would like to be with in a pod. We highlight that, besides out-grouping, there are issues in asking students for their pod preferences. We give evidence in an appendix why the following (desirable) property, stability, does not hold: “There are no two students that would prefer to be in each other’s pod.” The reason why this cannot be satisfied is that the change of pod of the two students might create a new pair of students that would like to change pods. The property, often called “stability” makes satisfying preferences hard.
Also, we show why students in general would want to misreport their preferences when facing a system that optimizes the assignment given stated preferences (manipulability). Manipulability in general is not bad—if all participants understand that their “preferences” should be chosen strategically. As this cannot necessarily be assumed, this property is hard to satisfy.
We conclude this article with a case study on clustering essential classes at MIT into pods.
Case Study: MIT
We start our analysis with a list of essential classes that was compiled by MIT administrators. (The administration did not specify whether the on-site visit of a class might be essential only for some students.) Using historical registration data from Academic Year 2017, we reconstruct which students would take at least one class on-site. We assign the students into pods of about 50 students and offer sufficiently many sections of courses to prevent class encounters between students in different pods.
Some classes from the list of essential classes had several hundred students. While we incorporated them in our analysis, these are candidates for lectures that might be offered online to limit meetings between pods.
Two important properties of the graph after deleting central classes can inform the definition of pods:
First, the majority of students take only one of the essential, non-central classes. Also, when disregarding the largest class that each student takes, students cluster nicely.
A Heuristic
Using these observations, we implement a way to define pods and sections:
- We first subdivide all students that take only one essential class into pods of 50 and offer one section per resulting pod.
- We then first disregard the largest classes until all connected components (hence all sets of students that have no chain of persons that pairwise share a class with one another) are less than 50 students.
- We then re-introduce large classes and use a (heuristic) clustering algorithm to cluster previously unassigned students.
This heuristic for the definition of pods yields an average size of pods of 34, and a number of (physical) sections per class 3.4; for large classes, this ratio is 5.3, for small classes 3. By running steps 1. and 3. on small classes first, then all three steps on large classes, one clusters in priority small classes and improves the performance of the clustering algorithm at step 3… The number of sections per class falls to 2.5 on average; it is 4 for large classes and 2.2 for small classes.
Since MIT departments also express their preferences for classes to be held in a unique section, we adapted this heuristic to cluster in priority students that take a class that shall not be duplicated. This imposes a significant burden on classes that can be duplicated, especially large ones, significantly increasing the number of subsections for these classes.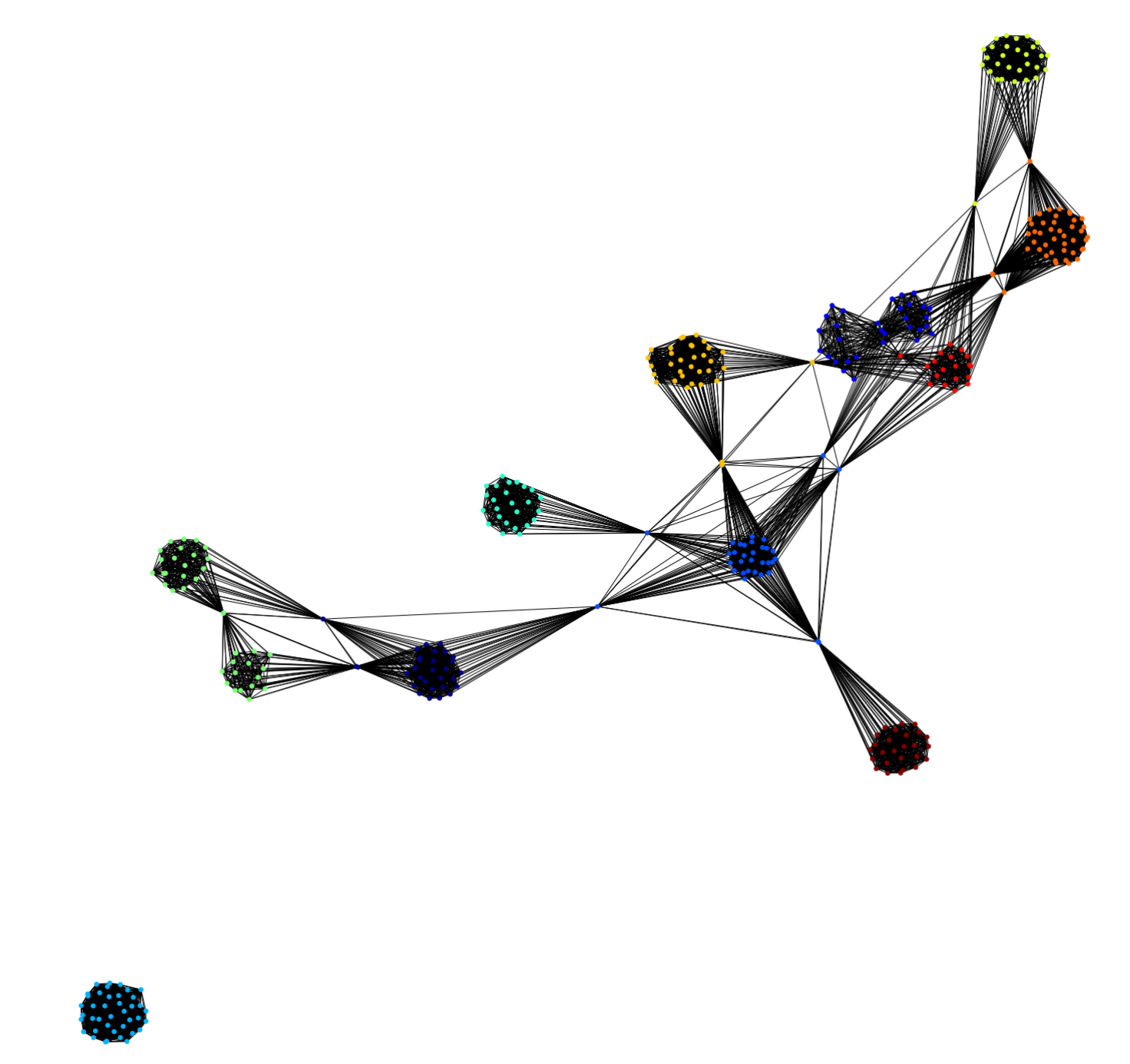
After removing a maximum number of students taking classes that shall be held only once, one can nicely cluster students taking small classes in pods of 50 or less. Some students appear to be “problematic” when they link together otherwise disconnected clusters.
While our method is certainly not giving us the optimal pod structure, it tells us that an upper bound on the price to pay to allow essential classes to be given on-site during academic year 2020-2021, is to have these classes divided in, on average, 2.5 sections per class.
We highlight weaknesses of this case study. First, it is not guaranteed that the historical (2017) registration data shares structure with the 2020 data. Furthermore, the above approach is not guaranteed to give a heuristic solution which has a guarantee to minimize the number of sections or the cases where a student cannot take a class on-site. (Indeed, this would be a computationally hard problem.)
To Sum Up
We believe that essential MIT classes could be held on site at a reasonable administrative cost, with students clustered in independent pods of average size ~30. Asking students to only take classes on-site that are necessary for their graduation might further alleviate some administrative constraints. A challenge of the design of pods, and, ultimately, of adherence, is the social component of pods. Good communication, also of our arguments against elicitation of student preferences, and socially-distanced meetings, might help to tackle this challenge.
Appendix: Problems with Asking for Student Preferences
Here, we give examples why asking students for their preferences on whom to be with in a pod might be challenging. We stay with examples to give intuition and use again our group of four students, Alice (A), Bob (B), Claire (C) and Daniel (D). We would like to cluster the four into two pods of two students, compatibility of clases is not an issue (but could add complications). Assume also that every student has one dearest friend, and they care first and foremost being together in a pod with them. We denote this by a a directed arrow.
They also have a second-dearest friend, which is the person that has them as their dearest friend. We show that for this setting, justified envy must exist. Finally, everyone prefers some other students with them in a pod to no-one in their pod. (Assignments with lonely students are unstable, as students could change with another lonely student.)
Instability
There are three possible pod assignments without lonely students: A and B and C and D could form a pod, A and C and B and D, or A and D and B and C. In the first case, B and D would like to change pods and in the second A and C would like to change. (In the “swapped pods” the changing students would get their dearest friend in their pod.) The third pod assignment puts A and B with their least preferred person in a pod, and they could change to get their second-dearest friend in a pod. This implies that there is justified envy – this persists in larger cases if there are some chains of students that have a preference for each other that is larger than the maximum pod size.
Manipulability
We now show that an algorithm that looks like it innocuously optimizes given the preferences might lead to incentives to misreport for agents. The algorithm we consider gives a score of 1 for any person that is in a pod with their first choice, a 2 for any person that is in a pod with their second choice and a 3 for any person that is in a pod with their third choice. Assume that ties are broken uniformly at random among score-minimizing pod assignments. Consider the following preferences:
A: D,B,C
B: A,D,C
C: D,B,A
D: A,C,B
where the lists are in decreasing preference, i.e., A would like to be with D most, then with B and least with C. For these preferences, the assignment that puts A and B, and C and D in a pod minimizes the score (with score 6). If D decided to report A,B,C, then a random pod assignment of either A and B, and C and D or A and D and B and C would be chosen (both are minimizers with score 7).
Hence, in this case, Daniel needs to think about what others play, and cannot “just” submit her preferences. This can, in the worst case, lead to inequity for students that do not submit their preferences in a sophisticated manner.
(For readers eager to learn more about these types of problems: The pod assignment problem is a generalization of the Stable Roommates Problem. It shares instability with the problem, and stronger results on manipulability can be proved.)
For more information please contact: Manon Revel, Andreas Haupt