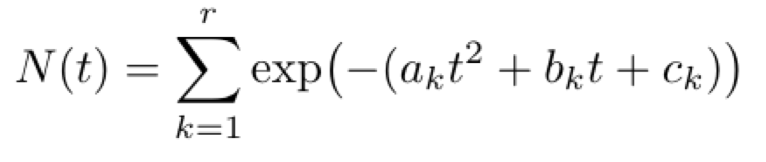Mixtures Matter
As recently discussed in the New England Journal of Medicine, most models used to predict key quantities related to COVID19 take one of two general approaches. They are either mechanistic and assume an underlying model such as a Susceptible-Infected-Recovered framework, or use a data-driven, non-mechanistic method to make predictions based on existing trends in the data.
While there is a significant discussion as to when each type of approach is to be used, many of the models currently being used, regardless of their general approach, tend to share one key assumption. They either implicitly or explicitly assume that the data will have only one apex.
From a global perspective, the idea that the number of confirmed cases in a population has only one peak does not seem to account for the fact that the virus has spread from community to community. For example, the spread of COVID19 began in Wuhan, China, and the Hubei province then locally saw exponential growth in the number of confirmed cases. Later, the virus spread from community to community across the globe, starting outbreaks afterwards in Italy and the United States. These communities then saw their own local exponential growth in the number of confirmed cases.
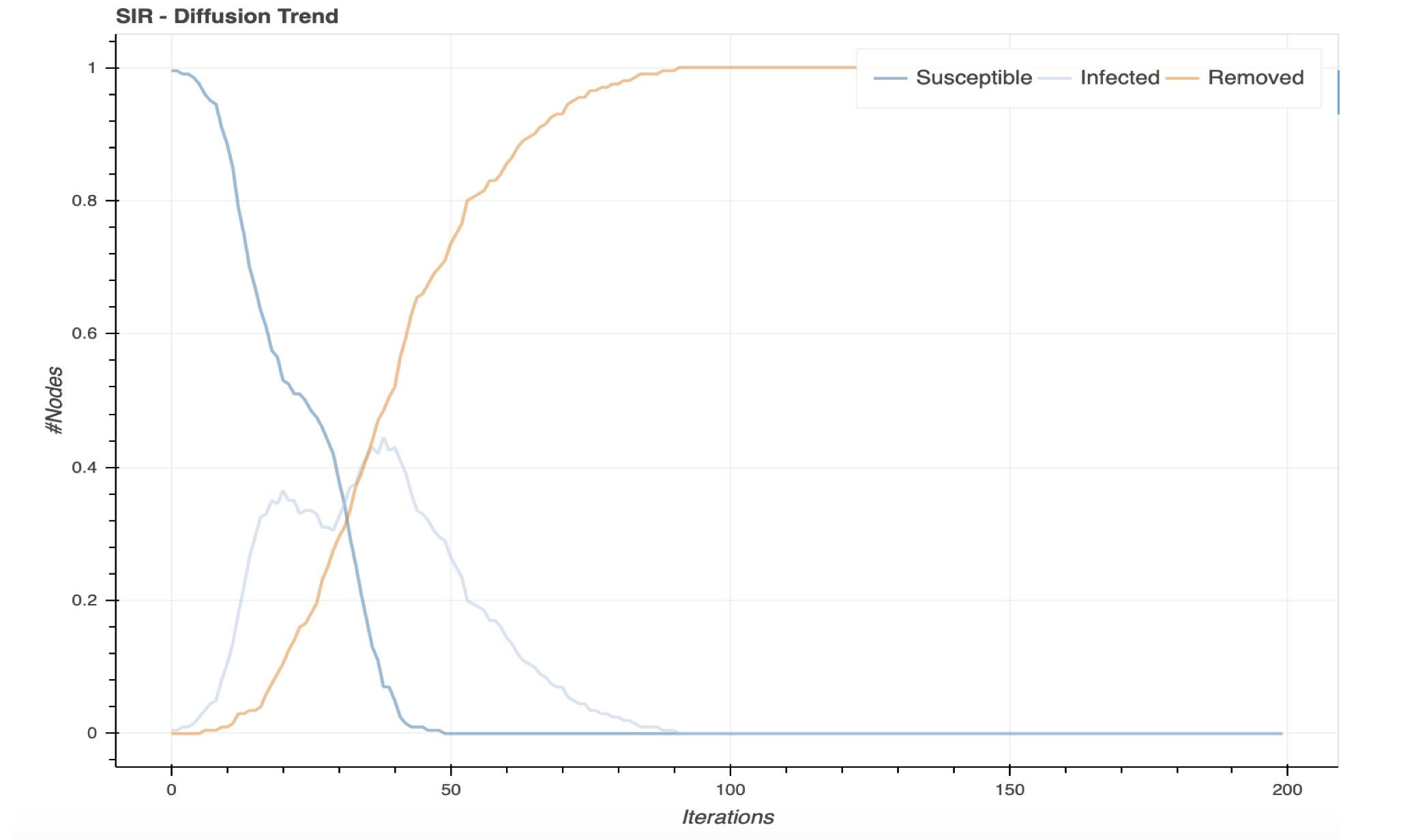
This underlying reasoning based on community structure asks us to consider a mechanistic model based on a Stochastic Block Model, a process to generate a random graph which explicitly accounts for community structure. We can form a graph that consists of two very densely connected communities which have few connections in between members of those communities. Then, we can consider how an SIR process would spread. Such an experiment results in the following plot.
The infected curve in the plot above shows two distinct local maxima in the number of infected nodes in this model, as a result of the epidemic starting to spread later in one community than the other.
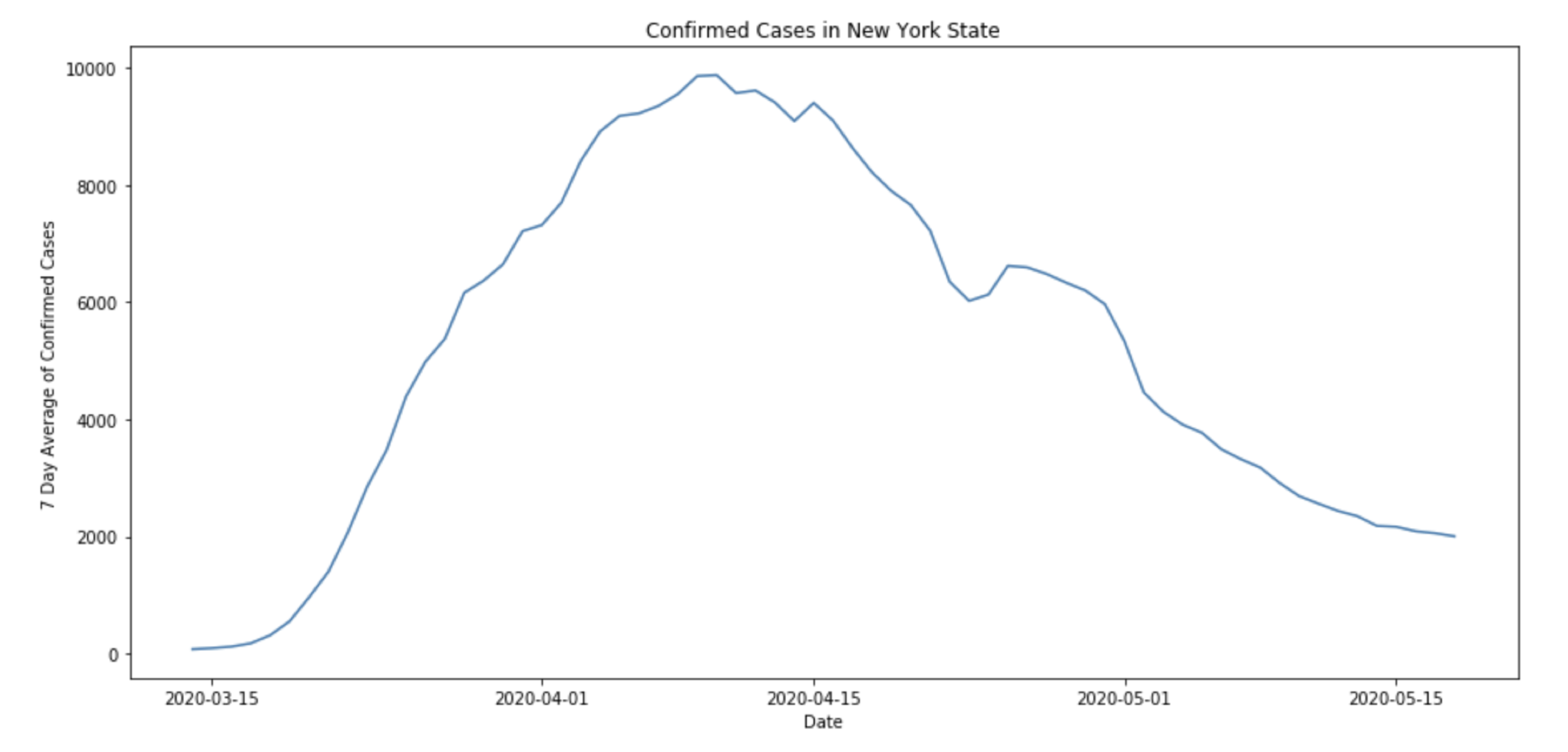
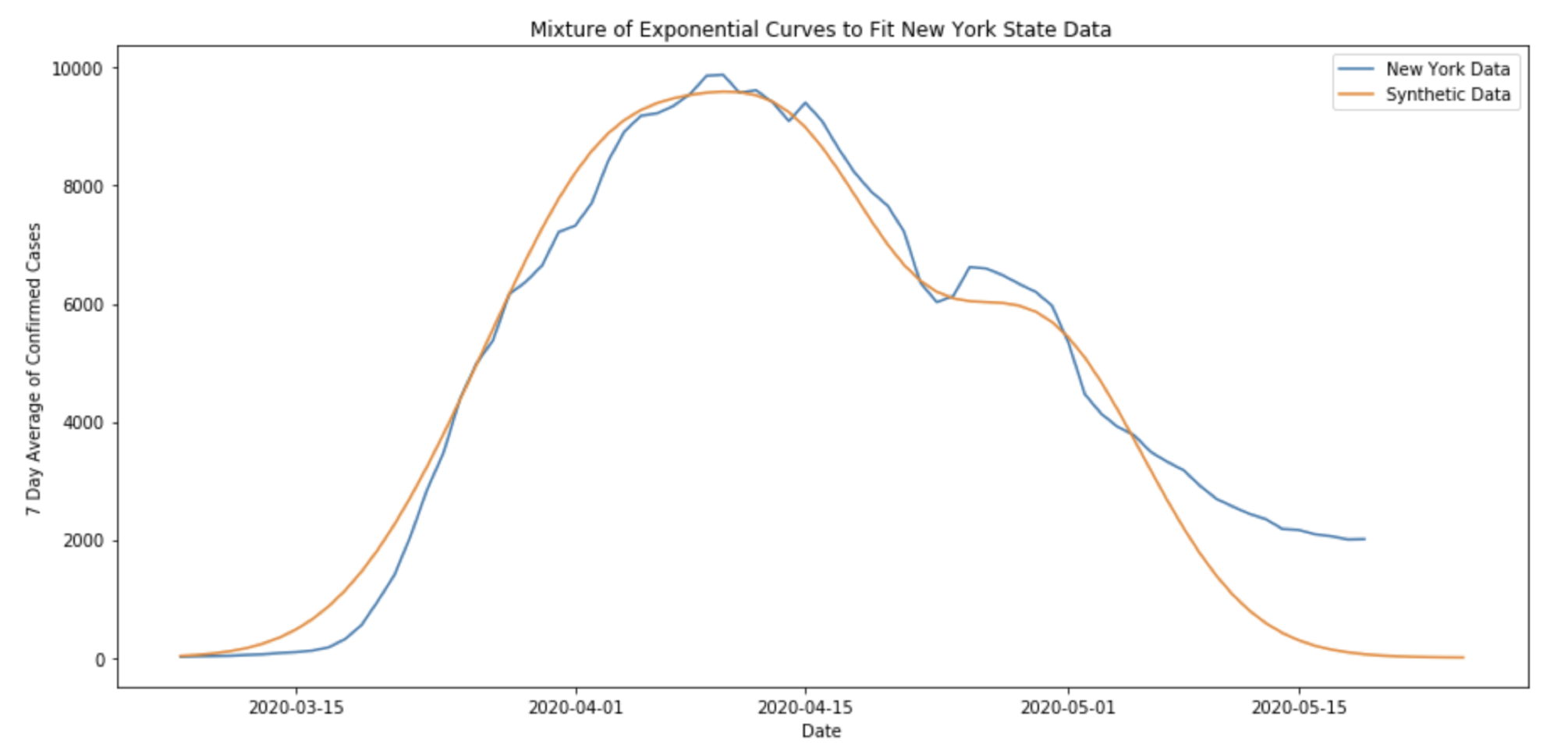
In fact, observed COVID19 data starts to show similar behavior to a mixture of SIR-like curves. Take, for example, the curve for confirmed cases in New York State.
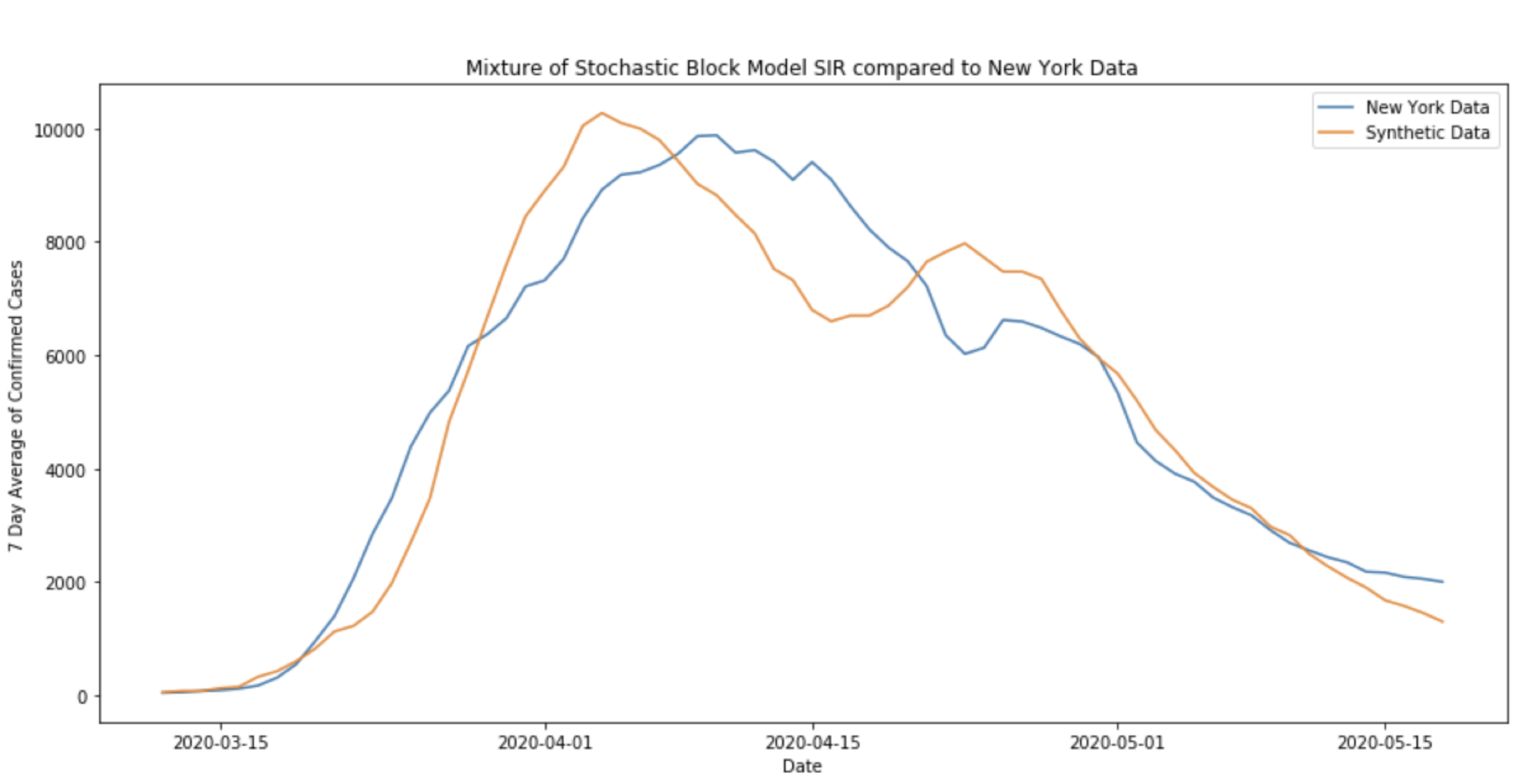
Here, even after taking a 7-day average of the case data, there is a noticeable “bump” in the number of confirmed cases in New York towards the end of April. In fact, this phenomena can be replicated using an SIR process on a graph like the one above.
The above plot admits the possibility that the irregularity in the New York state level data could be a result of COVID19 spreading first through one large community, and then later beginning to spread quickly through a smaller community.
From a non-mechanistic perspective, we see that prediction based upon the procedure above would amount to fitting the time series of confirmed cases to the set of functions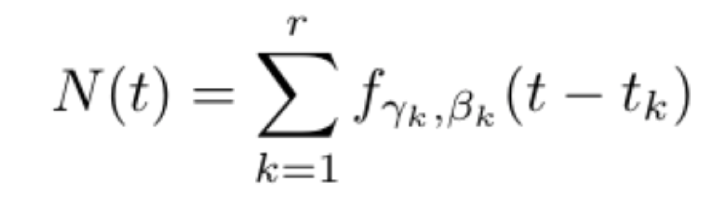
Where ![]() and
and ![]() parameterize the infected curve for an SIR model, and tk is a time shift.
parameterize the infected curve for an SIR model, and tk is a time shift.
This form has an interesting implication, in that key quantities in epidemic modeling, such as the reproduction number, no longer have a simple form. For example, in a typical SIR model with one community, we expect the effective reproduction model to decay as time progresses forward, due to the number of susceptible individuals in that community falling. However, when we assume that a curve is a mixture of SIR-like curves, the effective reproduction number will actually have more of a piecewise shape, and we will specifically notice an uptick in reproduction number as the number of new confirmed cases becomes dominated by a new community. Hence, we hope that this model will result in a better fit to data than single apex models, and better explain variability for example in the time series of reproduction numbers.
While the implication above is interesting, unfortunately the above class of functions may not be easily learned from data, as the closed form solution for the infected curve of an SIR model is non-trivial. Instead, in practice we can turn to another, more tractable function class:
This form proves to be easier to learn, and can also fit observed data quite well.
One key difference when working with mixtures of curves as opposed to learning a single curve, is that with enough mixtures, our function class becomes universal. It could potentially fit perfectly to any time series! This raises an important issue in that our method would not be falsifiable and hence provide no meaningful scientific insight beyond potentially being extremely good at fitting the data and perhaps prediction. Our hope is that by restricting to a small number of mixtures, we can develop a principled, falsifiable theory to model epidemics by taking into account mixtures. This will provide meaningful insights; for example, the emergence of mixtures may suggest the strengths of ‘inter-connection’ between communities helping towards epidemic management.
For further details, please contact Ali Jadbabaie, Arnab Sarker, and Devavrat Shah