In the Weeds: On Masks
The dispersal of droplets coupled with viral growth kinetics coupled with human behavior is an extremely complex problem. We do not expect our analysis to provide exact answers; rather in this analysis we seek guidelines that may help inform decisions. In that spirit, we have made a number of assumptions and approximations which are detailed below; we invite the reader to consider these carefully in determining whether these are acceptable for their purposes.
Characteristic length scales
Revisiting the droplet dynamics described in the original post, the settling velocity of a droplet at low Reynolds number is given by
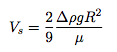where g is gravity, µ is the dynamic viscosity of the air, R is the radius of the droplet, and Δρ is the density difference between water and air. This can be used to estimate the settling time which in turn sets the distance the droplet diffuses before it hits the ground: x = (D tS)½. Here the diffusivity of our droplet random walker can be estimated as:
Where ϵ is the characteristic step size, Δt is the time between steps, and α = 2, 4, or 6 for 1-, 2-, and 3-dimensions, respectively. Combining these, we find an expression for the distance a droplet of radius R travels, which suggest a characteristic length scale in the problem, lc defined as:
This characteristic length scale is used to nondimensionalize all of the variables; x and R are scaled by 1/lc and p(R) and c(x) are scaled by lc.
Volume versus number fraction
In our analysis we have defined a concentration based on the number of droplets rather than the mass or volume of droplets. This choice was made because order of magnitude estimates suggest that we may exhale thousands of droplets in a single breath, but only tens (or possibly hundreds) of viral particles per minute. This implies that the expected number of particles per droplet is much less than one. Here we take a middle-of-the-road position and assume that viral particles are equally likely to hide in large or small droplets; hence, concentrations defined by number, rather than mass, are likely to be more useful. However, the truth of the matter is that we do not know how the probability of carrying a viral particle depends on droplet size e.g. there may be activities such as singing or shouting that draw air from deeper in the lungs and produce more fragmented droplets so smaller droplets have a higher probability of carrying the virus; or the virus may be uniformly dispersed in the emitted fluid so larger droplets are more likely to carry viral particles. Both scenarios seem plausible and we have not seen evidence to argue convincingly for either side. Hence for now we split the difference and assume that viral particles are equally likely to reside in small or large droplets. However, if evidence emerges that indicates that larger droplets are more likely to contain viral particles, it is straightforward to revise the calculation above to include volumetric concentration in which case the correction factor becomes (1-β)1/5.
Evaporation
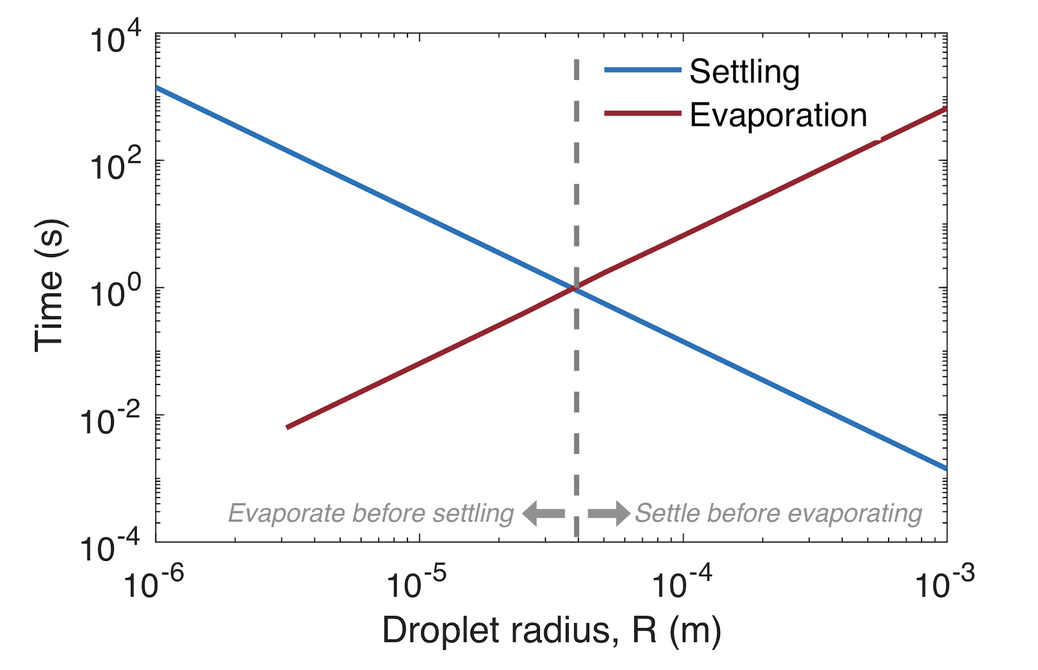
As the attentive reader has noticed, our calculations here have not accounted for the evaporation of droplets. Evaporation does indeed affect the distribution of droplet sizes in the cloud, however the time scale of evaporation is significantly faster than that of diffusion. This means that only the largest droplets reach the ground before evaporating, where the cutoff size for “large” droplets is approximately 50 microns (less in high humidity). Those that do reach the ground, do so at a very short distance from the source (x ~ 5 cm).
Estimates of droplet evaporation times in unsaturated air at 18° C based on Wells (1934) and settling times according to our derivations above. Droplets smaller than a certain radius will evaporate before they settle, and remain in the air as droplet nuclei.
The smaller droplets evaporate within fractions of a second, and can remain in the air as droplet nuclei, with radii that typically fall in the size range 0.5-5 microns. These droplet nuclei will then diffuse in the way described above, and settle to the ground at a distance that is inversely proportional to the nucleus radius. In other words, evaporation affects the size of a droplet, but not the manner in which it moves away from the source.
This means that the concentration of virus-carrying droplets c(x) at the length scales we are interested in turns out to depend on the distribution p(R) of droplet nuclei (rather than that of exhaled droplets). Since the size range of droplet nuclei is smaller than that of exhaled droplets, the effect of evaporation is a flattening of the probability distribution, rendering it more similar to the uniform distribution used to derive our rule of thumb.
Directionality
In the calculation above we have assumed that the particles are uniformly dispersed around the source. Again it is straightforward to modify the calculation to include directionality; instead of distributing the particles around a circle of radius x, we distribute them across an arc; the length of this arc drops out of the calculation (since it appears in both the masked and the unmasked estimate) and the adjustment to x0 is the same as in the uniformly dispersed case.
Initial velocity of exhaled droplets
The Reynolds number for a 5 micron droplet exhaled at speeds on the order of 1 m/s, is approximately 0.3, which implies that the dynamics are dominated by viscous effects and the initial velocity is rapidly damped out. In the absence of air currents, we can estimate the distance that an exhaled droplet travels before it is stopped by viscous drag, which provides a reasonable estimate of the region in which the initial velocity plays a role. Balancing mass times acceleration with viscous drag yields a characteristic time scale t ~ m/(6πµR). Multiplying this by the characteristic exhalation velocity, we find that the droplet travels approximately 300 microns before it grinds to a halt. This is a tiny fraction of the two meters that the droplet travels, hence we can safely neglect the initial velocity of the droplet in our estimates.
